How To Flip A Fraction

Fractions

10 Dividing Fractions

Dividing fractions follows like logic to multiplying fractions. Information technology involves working with the numerators and denominators separately. One time you have done your initial calculations, you put it all together to get your respond. There is a lilliputian twist, though, that we'll have to examine equally we piece of work through some questions.

Before we become to all that, allow'south get-go past revisiting dividing whole numbers, and and then nosotros'll work our way up to fractions.

Start with xx screwdrivers:

At present split up those 20 screwdrivers by 10 (or into groups of x).

[latex]\LARGE20÷10=2[/latex]

You end upward with ii groups of 10.

20 screwdrivers in two lines. There are 10 screwdrivers in each line

Now divide those 20 screwdrivers by v (or into groups of five).

[latex]\LARGE20÷5=four[/latex]

You end up with 4 groups of 5.

20 screwdrivers divided into groups of 5. There are 4 groups total

Now divide those 20 screwdrivers by two (or into groups of 2).

[latex]\LARGE20÷2=10[/latex]

You end up with ten groups of ii.

20 screwdrivers with two screwdrivers in each group. There are 10 groups total

Have a look at the math here. Do you come across a pattern? What did you come with? Did you find that, when yous accept your original amount (in this case, 20) and divide it by a number that continues to go smaller (10, then five, and then ii), we finish up with an answer that gets larger.

[latex]\LARGE20÷ten=2[/latex]

[latex]\LARGE20÷five=4[/latex]

[latex]\LARGE20÷two=10[/latex]

Follow this logic into fractions, keeping in mind that fractions are non just less than ten, 5, and 2, but i. Using this pattern, we determine that dividing the 20 screwdrivers by a number less than ane would go us a larger answer than if we divided the 20 by ten, 5, or 2.

Effort this. Take the 20 screwdrivers, and split them by ½. What do you think your answer will be?

[latex]\LARGE20÷\dfrac{1}{2}=?[/latex]

Post-obit our logic, the answer should be more than than ten, and in fact, it is.

[latex]\LARGE20÷\dfrac{i}{2}=twoscore[/latex]

This does not hateful that we terminate upwardly with twoscore screwdrivers, though. What information technology means is that we end up with xl parts of screwdrivers. You have to imagine that each of the screwdrivers were split into 2. Twenty screwdrivers split in one-half would give us 40 pieces in the cease. The question at present becomes, how do we practise this mathematically? The answer lies in using what is known as a reciprocal. Here is the definition.

Reciprocal: A number that has a relationship with another number such that their product is ane.

This means that, when you take a number such as 5 and then multiply it by its reciprocal, you volition end upwardly with an answer of 1. Nosotros'll start with the whole number five. We could besides write the number v as a fraction.

[latex]\LARGE5=\dfrac{5}{1}[/latex]

Using our definition of reciprocal, nosotros need to detect a number that, when multiplied past ⁵/_i, gives us an respond of ane.

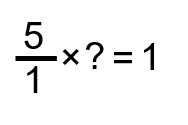
5 over 1 times blank = 1

To find the reply, we have to get back to multiplying fractions. Call up that, when we multiply fractions, nosotros just multiply the numerators together and so multiply the denominators together. From this, nosotros can conclude that:

[latex]\Large\dfrac{5}{ane}\times\dfrac{one}{5}=1[/latex]

In the stop, to find the reciprocal of a fraction, we simply have the numerator and brand information technology the denominator and take the denominator and make information technology the numerator. Essentially, we are just flipping the fraction around. Here are some more examples of reciprocals.

[latex]\Large\dfrac{3}{eight}\text{ and }\dfrac{viii}{3}[/latex]

[latex]\Large\dfrac{two}{9}\text{ and }\dfrac{ix}{ii}[/latex]

[latex]\Big\dfrac{24}{17}\text{ and }\dfrac{17}{24}[/latex]

Okay, so now that nosotros have the reciprocal issue out of the way, the question then becomes, why do we need reciprocals in the first identify? Well, the reply lies in the dominion for dividing fractions.

A chalkboard message that reads, Know the rules!

The rule for dividing fractions is yous accept the beginning fraction and multiply it by the reciprocal of the 2d fraction. Yes, yous heard that right: to divide, you end up multiplying, just only after outset flipping the second fraction effectually.

Flipping the 2d fraction around (finding its reciprocal) changes the value of the equation. In club to keep the equation mathematically the same, we have to change the segmentation question into a multiplication question. Take a look at the following instance to meet how this is done.

[latex]\Big\dfrac{one}{2}÷\dfrac{3}{8}=?[/latex]

Stride 1: Put the question into a grade that you can work with. This involves finding the reciprocal of the 2d fraction and then multiplying it by the kickoff.

[latex]\LARGE\text{The reciprocal of }\dfrac{iii}{8}\text{ is }\dfrac{8}{3}[/latex]

[latex]\Large\text{Check: }\dfrac{3}{8}\times\dfrac{viii}{three}=\dfrac{24}{24}=i[/latex]

So we stop upwardly with:

[latex]\LARGE\dfrac{one}{2}÷\dfrac{three}{eight}\text{ becomes }\dfrac{1}{two}\times\dfrac{viii}{3}=?[/latex]

Footstep 2: Follow the same procedure every bit nosotros did when multiplying fractions. Multiply the numerators together and then multiply the denominators together.

Multiply the numerators together

[latex]\LARGE1\times8=8[/latex]

Multiply the denominators together

[latex]\LARGE2\times3=6[/latex]

Step 3: Accept these answers and put them back into a fraction.

[latex]\Large\dfrac{1}{2}\times\dfrac{8}{3}=\dfrac{viii}{vi}[/latex]

Step four: Put the answer into everyman terms and then into a mixed number, if necessary.

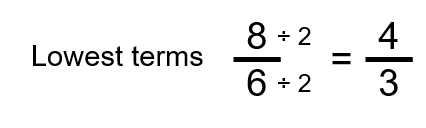
Reduce 8 over 6 into lowest terms by dividing the numerator and the denominator each by 2 to get 4 over 3

[latex]\LARGE\dfrac{iv}{3}=1\dfrac{1}{3}\text{ Mixed number}[/latex]

Final answer:

[latex]\LARGE\dfrac{1}{2}÷\dfrac{3}{8}=1\dfrac{1}{3}[/latex]

[latex]\LARGE\dfrac{5}{nine}÷\dfrac{vii}{4}=?[/latex]

Footstep 1: Put the question into a form that you can work with. This involves finding the reciprocal of the second fraction and then multiplying it past the first.

[latex]\Large\dfrac{5}{9}÷\dfrac{vii}{iv}\text{ becomes }\dfrac{5}{9}\times\dfrac{4}{7}[/latex]

Step ii: Multiply the numerators together and so multiply the denominators together.

Multiply numerators together

[latex]\LARGE5\times4=20[/latex]

Multiply denominators together

[latex]\LARGE9\times7=63[/latex]

Stride 3: Take these answers and put them back into a fraction.

[latex]\LARGE\dfrac{5}{9}\times\dfrac{iv}{7}=\dfrac{20}{63}[/latex]

Step 4: Put the answer into lowest terms and so into a mixed number, if necessary. In this example, the answer is both in lowest terms and is a proper fraction already, and so nosotros are done.

[latex]\Big\dfrac{5}{9}÷\dfrac{7}{four}=\dfrac{twenty}{63}[/latex]

Exercise Questions

Endeavor these do questions and accept a await at the video answers to run into how you did.

[latex]\Large\dfrac{7}{viii}÷\dfrac{7}{16}=[/latex]

[latex]\LARGE4\dfrac{vii}{8}÷2\dfrac{3}{4}=[/latex]

Annotation: This one is slightly dissimilar from what we take been doing, as information technology involves dividing mixed numbers. What practise y'all call back you are going to have to do when dealing with this?

ANSWER: Y'all have to change the mixed number into an improper fraction start. So you tin can work through the question the same way we accept been doing before.

How To Flip A Fraction,

Source: https://opentextbc.ca/mathfortrades1/chapter/dividing-fractions/#:~:text=In%20the%20end%2C%20to%20find,some%20more%20examples%20of%20reciprocals.

Posted by: fosterfenly1938.blogspot.com